Hero image for the blog post
Back to blog

Numpy QuadDType: Quadruple Precision for Everyone

Published September 30, 2024

SwayamInSync

SwayamInSync

Swayam Singh

Picture this: You're a scientist, working on complex simulations that push the boundaries of numerical precision. You fire up your trusty NumPy-powered Python script, eagerly anticipating the results. But then... your calculations start producing unexpected errors. You've just stumbled into the realm of floating-point precision limitations.

Hi there! I'm Swayam Singh, and for the past three months, I've been developing numpy_quaddtype with Nathan Goldbaum, a true cross-platform quadruple precision datatype for NumPy. In this blog post, we'll explore why such high precision is sometimes necessary, dive into the technical aspects of numpy_quaddtype, and discuss its potential applications. Whether you're a quantum physicist, a financial modeler, or just curious about numerical computing, this post will give you insights about current precision limitations in NumPy and how we are resolving them.

So buckle up and grab your favorite beverage (might I suggest a Quad Espresso?)

Table of Contents

The Long Double Dilemma in NumPy

The np.longdouble dtype in NumPy has become a significant pain point for developers and users alike. Ralf Gommers, a core NumPy Maintainer, highlighted several critical issues that make long double support "extremely painful to maintain, probably far more than justified."

  1. Cross-Platform Inconsistency

The long double type varies dramatically across platforms:

  • Windows & macOS: 64-bit (same as double)
  • Linux (x86/x86_64): 80-bit
  • Some architectures (IBM Power9): True 128-bit quadruple precision

This inconsistency leads to portability issues and unexpected behavior, read more about this at NumPy: Issue #14574.

Meme showing different precision levels as Spider-Man characters
Figure: Visual representation of different precision levels in computing

  1. Build Complications Building NumPy, especially on Windows, has become increasingly complex due to np.longdouble:

    • MSVC uses 64-bit long double
    • Mingw-w64 defaults to 80-bit long double

    This discrepancy necessitates dealing with multiple toolchains and compiler patches, significantly increasing the maintenance burden. A detailed discussion of this issue can be found at NumPy: Issue #20348:

  2. Non-Standard Format NumPy supports 9 different binary representations for long double, each requiring specialized code:

    This complexity makes it challenging to implement and maintain, even in build systems like Meson, more about it at Meson: Issue #11068.

  3. Maintenance Overhead The NumPy team spends a disproportionate amount of time addressing long double-related issues, as well as dealing with hard-to-diagnose build issues, especially on Windows :

  4. Limited Practical Benefits Despite these challenges, the benefits of long double are questionable:

    • On Windows and macOS, it's functionally identical to double, only consuming more memory with padded bits.
    • On Linux, it provides only a modest precision increase (80-bit vs 64-bit).

  5. Hidden Complexity The long double issue extends beyond the user-visible dtype. It's also baked into the libnpymath static library shipped with NumPy, adding another layer of complexity to any potential solutions NumPy Issue #20880.

Given these issues, the NumPy community is at a crossroads. The current approach to long double support is proving to be increasingly problematic and difficult to maintain. It's clear that a new direction is needed to ensure the long-term stability and usability of NumPy across different platforms.

As we move forward, the community is considering several potential solutions, from full deprecation to developing a true cross-platform quadruple precision dtype.

In our next section, we'll explore how numpy_quaddtype aims to address these issues, promising a future where high-precision computing in Python doesn't come with a side of maintenance headaches.

Introducing Numpy-QuadDType

NumPy-QuadDType (numpy_quaddtype) is a custom data type (dtype) implementation for NumPy that provides true quadruple precision floating-point arithmetic across different platforms. This project aims to address the long-standing issues with np.longdouble by offering a consistent, high-precision floating-point type regardless of the underlying system architecture with also providing backwards compatibility of long double.

The core of numpy_quaddtype is built around two key components:

  1. A scalar type QuadPrecision that represents individual quadruple-precision scalars.
  2. A NumPy dtype QuadPrecDType that allows these quadruple-precision scalars to be used in NumPy arrays and operations.

What sets numpy_quaddtype apart is its dual-backend approach:

  • SLEEF (SIMD Library for Evaluating Elementary Functions): This backend uses the Sleef_quad type from the SLEEF library, providing true 128-bit quadruple precision.
  • Long Double: This backend uses the native long double type, which can offer up to 80-bit precision on some systems allowing backwads compatibility with np.longdouble.

If the compiler natively supports IEEE 754 quad precision Floating Point type, then Sleef_quad is an alias of that data type. Otherwise, it defines a 128-bit data type for retaining a number in IEEE 754 Quad-Precision data format.

This flexibility allows numpy_quaddtype to provide the best available precision across different platforms while maintaining a consistent interface.

By addressing these goals, numpy_quaddtype not only solves the immediate issues surrounding np.longdouble but also paves the way for more robust and precise numerical computing in Python. In the following sections, we'll delve deeper into how these goals are achieved through the technical implementation of numpy_quaddtype.

The Inner Workings of numpy_quaddtype

numpy_quaddtype is built on a flexible architecture that marries high precision with cross-platform compatibility. At its core lies the QuadPrecisionObject, a chameleon-like structure that can switch between two forms:


typedef union {
Sleef_quad sleef_value;
long double longdouble_value;
} quad_value;
typedef struct {
PyObject_HEAD
quad_value value;
QuadBackendType backend;
} QuadPrecisionObject;

This dual-nature allows us to leverage the full 128-bit precision of SLEEF when available, while maintaining backwards compatibility with np.longdouble.

To integrate seamlessly with NumPy, we've created the QuadPrecDTypeObject:


typedef struct {
PyArray_Descr base;
QuadBackendType backend;
} QuadPrecDTypeObject;

This structure acts as a bridge, allowing our high-precision numbers to work harmoniously within NumPy arrays and operations.

The backend selection is handled by a simple enum:


typedef enum {
BACKEND_INVALID = -1,
BACKEND_SLEEF,
BACKEND_LONGDOUBLE
} QuadBackendType;

This flexibility enables numpy_quaddtype to provide optimal precision across different platforms while maintaining a consistent interface. Users can select their preferred backend at runtime:


>>> import numpy as np
>>> import numpy_quaddtype as npq
# Using SLEEF backend (default)
>>> x = npq.QuadPrecision(3.5)
>>> x = npq.QuadPrecision(3.5, backend='sleef')
>>> repr(x)
QuadPrecision('3.5e+000', backend='sleef')
# Using longdouble backend
>>> y = npq.QuadPrecision(2.5, backend='longdouble')
>>> repr(y)
QuadPrecision('2.5e+000', backend='longdouble')
# Creating a NumPy array with QuadPrecision dtype
>>> z = np.array([x, x], dtype=npq.QuadPrecDType()) # SLEEF
>>> print(z)
[QuadPrecision('3.5e+000', backend='sleef')
QuadPrecision('3.5e+000', backend='sleef')]
>>> z = np.array([y, y], dtype=npq.QuadPrecDType("longdouble")) # longdouble
>>> print(z)
[QuadPrecision('2.5e+000', backend='longdouble')
QuadPrecision('2.5e+000', backend='longdouble')]

Under the hood, numpy_quaddtype manages memory efficiently for both aligned and unaligned memory access. This is crucial for performance, especially when dealing with large arrays or complex computations. We've also implemented specialized strided loop functions for various operations.

Casting operations

Casting operations are another critical component. We've implemented a range of casts between QuadPrecision and other NumPy types, ensuring smooth interoperability:


# NumPy to QuadPrecision
>>> numpy_array = np.array([1.5, 2.7, 3.14])
>>> quad_array = numpy_array.astype(npq.QuadPrecDType())
>>> print(quad_array)
[QuadPrecision('1.5', backend='sleef') QuadPrecision('2.7', backend='sleef')
QuadPrecision('3.14', backend='sleef')]
# QuadPrecision to NumPy
>>> quad_value = npq.QuadPrecision("3.14159265358979323846")
>>> numpy_float = np.float64(quad_value)
>>> print(numpy_float)
3.141592653589793
# Mixing types in operations
>>> result = quad_array + numpy_array # Automatically promotes to QuadPrecision
>>> print(result)
[QuadPrecision('3.0', backend='sleef') QuadPrecision('5.4', backend='sleef')
QuadPrecision('6.28', backend='sleef')]

For preserving precision during casting it is recommended to pass input as a string

working with QuadPrecision numbers is as straightforward as working with any other NumPy type. The casting operations handle the heavy lifting behind the scenes, allowing you to focus on your computations rather than type management.

Universal Functions (UFuncs)

numpy_quaddtype implements a wide range of universal functions, covering unary operations (like square root or exponential), binary operations (addition, multiplication, etc.), and comparison operations. These ufuncs are the backbone of NumPy's efficient array operations, and we've ensured that QuadPrecision numbers work seamlessly with them. Here's a taste of how you might use these ufuncs:


>>> a = npq.QuadPrecision(2.0)
>>> b = npq.QuadPrecision(3.0)
# Unary operation
>>> print(np.sqrt(a)) # QuadPrecision square root
1.4142135623730950488016887242097
# Binary operation
>>> print(a + b) # QuadPrecision addition
5.0
# Comparison
>>> print(a < b) # QuadPrecision comparison
True
# Using with NumPy arrays
>>> quad_array = np.array([a, b], dtype=np.QuadPrecDType())
>>> print(np.exp(quad_array)) # Element-wise exponential
['7.38905609893065022723042746057501 ', '20.0855369231876677409285296545817 ']

These operations look identical to standard NumPy operations, but under the hood, they're using the full precision of QuadPrecision numbers.

Precision in Printing: The Dragon4 Algorithm

When it comes to displaying QuadPrecision numbers, accuracy is paramount. That's where our customized implementation of the Dragon4 algorithm comes in. Dragon4 is a sophisticated algorithm for converting binary floating-point numbers to their decimal representations, ensuring that the printed value is as close as possible to the true value of the number in memory.

  • Without Dragon4

    >>> a = npq.QuadPrecision("1.123124242")
    >>> print(a)
    1.123124242000000000000000000000000e+00

  • With Dragon4

    >>> a = npq.QuadPrecision("1.123124242")
    >>> print(a)
    1.123124242

Our implementation of Dragon4 for numpy_quaddtype is a significant improvement over the previous approach used for np.longdouble. We've eliminated complex platform-specific branching that was used to handle different binary representations of np.longdouble, resulting in a more streamlined, maintainable and consistent output across different platforms.

By addressing these various aspects - from low-level memory management to high-level NumPy integration and precise number representation - numpy_quaddtype provides a robust and flexible solution for high-precision arithmetic in Python. It offers the extreme accuracy you need for demanding computations, wrapped in the familiar and user-friendly NumPy interface you already know and love.

Precision and Accuracy

In the world of high-precision computing, not all floating-point representations are created equal. numpy_quaddtype offers two backends, each with its own precision characteristics. Let's break them down:

SLEEF Backend Precision

The SLEEF (SIMD Library for Evaluating Elementary Functions) backend provides true 128-bit quadruple precision. Here's what that means in practice:

  • Significand: 113 bits
  • Exponent: 15 bits
  • Sign: 1 bit

This translates to approximately 34 decimal digits of precision. To put this in perspective, if you were measuring the diameter of the observable universe (approximately 8.8 x 1026 meters), you could do so with precision down to the width of a proton!

Long Double Backend Precision

The long double backend's precision varies depending on the platform:

  • On most x86 and x86-64 Linux systems: 80-bit extended precision

    • Significand: 64 bits
    • Exponent: 15 bits
    • Sign: 1 bit
    • This provides about 18-19 decimal digits of precision

  • On Windows and some other platforms: Often identical to double precision (64 bits)

    • Significand: 52 bits
    • Exponent: 11 bits
    • Sign: 1 bit
    • This provides about 15-17 decimal digits of precision

ULP Analysis

ULP (Unit in the Last Place), is a measure of the spacing between floating-point numbers and is crucial for understanding the accuracy of floating-point operations. In numpy_quaddtype, the ULP characteristics vary not just between backends, but also between different operations.

For the SLEEF backend:

  • Basic arithmetic operations (add, subtract, multiply, divide), ULP error bound ≤ 0.5000000001
  • Transcendental functions (e.g., sine, cosine), ULP error bound ≤ 1.0

This means that for basic arithmetic near 1, the SLEEF backend can provide results accurate to about 33-34 decimal places, while transcendental functions maintain accuracy to about 32-33 decimal places.

This level of detail in ULP analysis is particularly relevant for applications where the accumulation of small errors over many operations can lead to significant discrepancies. For instance, in numerical simulations or financial modeling, understanding these ULP characteristics can help in choosing the most appropriate functions and in estimating the overall accuracy of complex calculations.

Testing and Applications

To rigorously evaluate the performance and capabilities of numpy_quaddtype, we implemented several challenging applications to showcase the power of quad-precision arithmetic but also demonstrate the cross-platform consistency of our implementation.

Mandelbrot Set: Exploring the Depths of Chaos

One of the most visually striking applications of high-precision arithmetic is in exploring the Mandelbrot set. This famous fractal serves as an excellent stress test for floating-point precision, as zooming into its intricate structures requires increasingly precise calculations.

We generated Mandelbrot set visualizations at an extreme zoom level of 1020, centered at the coordinates -1.749624030987687 + 0.0i, with 1000 iterations. The results are remarkable:

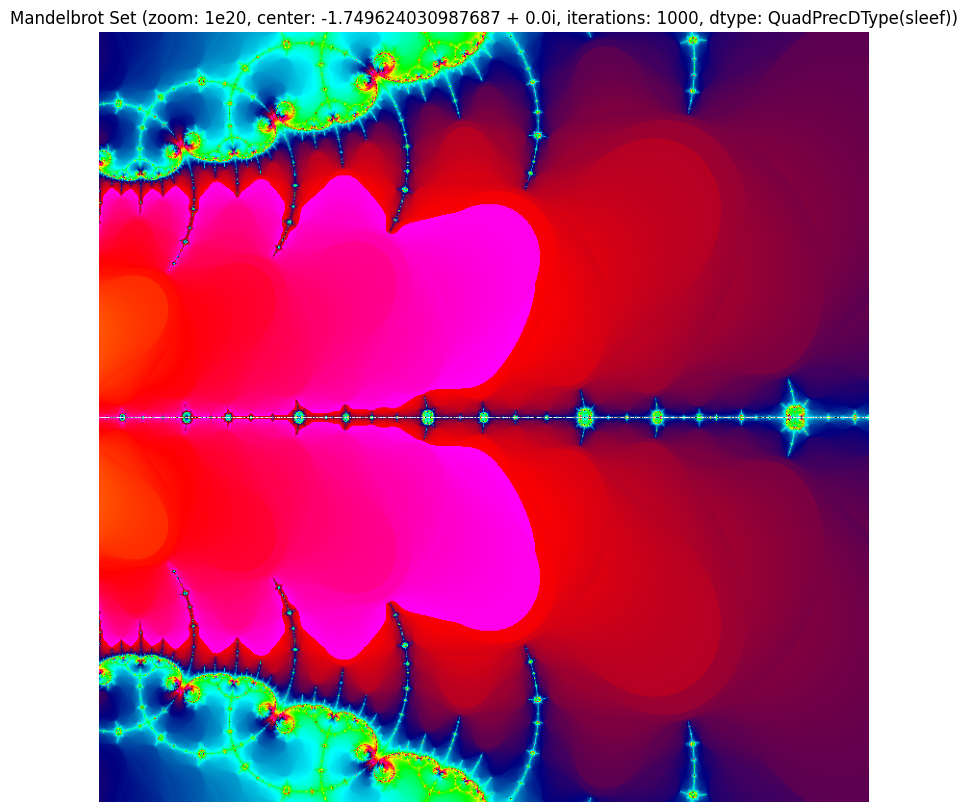
Mandelbrot set zoom at 1e20 using Quad-Precision SLEEF backend
Figure 2: Mandelbrot set at 1e20 zoom using numpy_quaddtype with SLEEF backend

Using the SLEEF backend of numpy_quaddtype, we achieved stunning detail and clarity even at this extreme magnification. The image reveals intricate structures, delicate filaments, and complex patterns that would be lost with lower precision calculations.

For comparison, we generated the same view using standard double-precision floating-point numbers (np.float64) and extended-precision long double:

Mandelbrot set zoom at 1e20 using double-precision floating-point
Figure 3a: Mandelbrot set at 1e20 zoom using np.float64
Mandelbrot set zoom at 1e20 using long double precision
Figure 3b: Mandelbrot set at 1e20 zoom using np.longdouble

The difference is stark. Both version loses all details, resulting in large blocks of solid color. This dramatically illustrates the limitations of 64-bit floating-point arithmetic and system dependent long double when pushed to these extremes.

Quantum Harmonic Oscillator for Diatomic Molecules

We applied numpy_quaddtype to model the quantum harmonic oscillator for diatomic molecules (Hydrochloric acid in our case).

We compared the performance of numpy_quaddtype against standard double-precision (np.float64) calculations. The results, visualized in two key graphs, highlight the significant advantages of quad-precision arithmetic in quantum mechanical calculations.

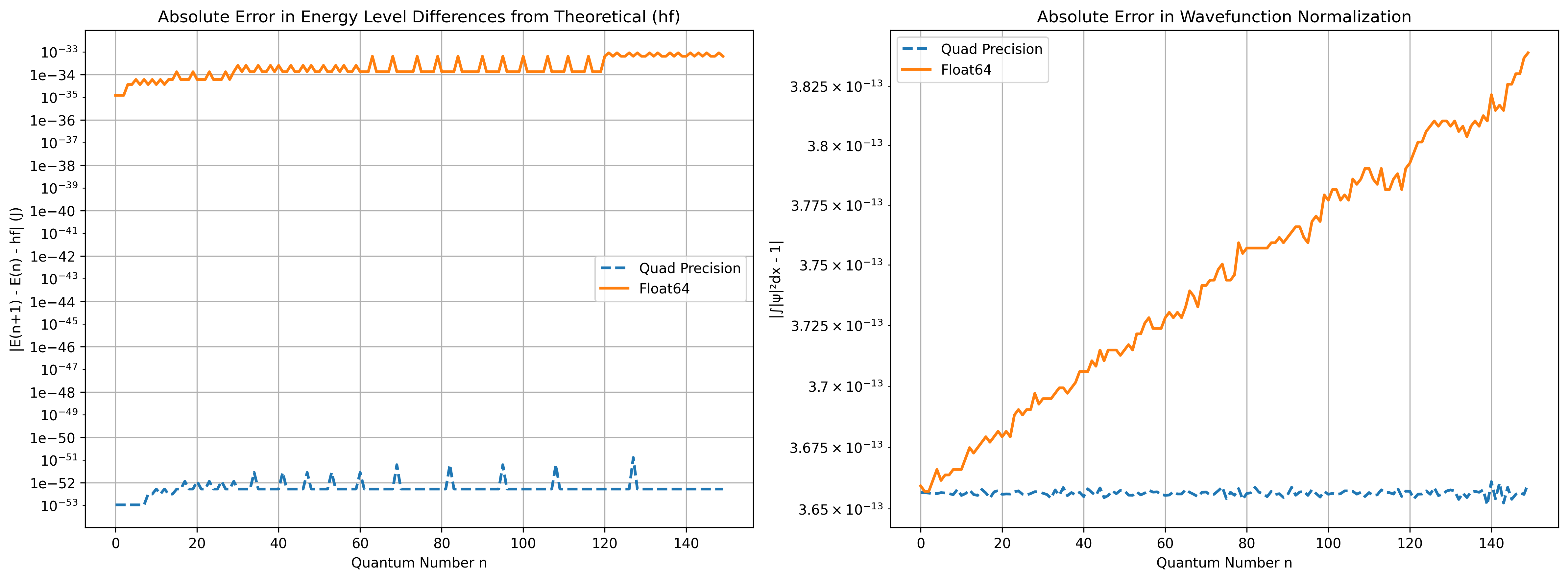
Comparison of Quantum Harmonic Oscillator calculations using np.float64 and numpy_quaddtype
Figure 4: Comparison of Quantum Harmonic Oscillator calculations for HCl molecule using np.float64 and numpy_quaddtype
  1. Absolute Error in Energy Level Differences
    • Quad Precision: Maintains extremely low error, consistently around 10-52 to 10-53 J across all quantum numbers, demonstrating exceptional stability and accuracy.
    • Float64: Shows significantly higher error, ranging from 10-34 to 10-33 J, with a slight upward trend for higher quantum numbers, indicating gradual precision loss.
  2. Absolute Error in Wavefunction Normalization
    • Quad Precision: Exhibits remarkably stable error around 3.65 × 10-13, ensuring consistent wavefunction validity across all quantum states.
    • Float64: Starts near quad precision levels but shows a clear upward trend for higher states, suggesting accumulating inaccuracies.

Current Status And Next Steps

As of this writing, numpy_quaddtype has reached a significant milestone. It's ready for use, supporting most major operations and integrating well with NumPy. As we've demonstrated with our Mandelbrot set visualizations and quantum harmonic oscillator calculations, it's capable of handling demanding computational tasks that require high precision.

However, like any new software project, there's still room for improvement and expansion. During development, we identified several areas in NumPy's dtype C-API that could be enhanced to better support custom dtypes like ours (NumPy Issue #27231)

Looking ahead, we have several key objectives:

  1. Package Distribution: We're preparing to release numpy_quaddtype as Python wheels, which will be available for installation via PyPI and as a conda package. This will make it easily accessible to the wider Python scientific computing community.
  2. Community Engagement: We plan to make a public announcement about numpy_quaddtype and actively seek feedback from the community. User experiences and suggestions will be crucial for guiding future improvements.
  3. NumPy Enhancement Proposal (NEP): We're drafting a NEP to formally propose the integration of numpy_quaddtype into the NumPy ecosystem. This process will allow for thorough discussion and review by the NumPy community.
  4. Future Backend Optimization: We plan to evaluate TLFloat, a C++ template library for floating-point operations, as a potential replacement for SLEEF in future versions. TLFloat offers IEEE 754 compliant operations with correctly rounded results for arithmetic operations and 1-ULP accuracy for other math functions across various precisions. This future exploration aims to further enhance numpy_quaddtype, particularly when guaranteed correctly-roundeded results are required.

numpy_quaddtype will continue to be an active development project under the NumPy umbrella. We're committed to refining and expanding its capabilities based on user needs and emerging requirements in the scientific computing community. We look forward to seeing how the community puts this new capability to use and hearing your feedback as we continue to improve and expand its functionality.

Stay tuned for updates, and happy computing! Remember, in the world of numerical analysis, precision is not just a luxury—it's often a necessity.

Conclusion

These past three months have been an extraordinary journey of learning and innovation. None of this would have been possible without the exceptional guidance and unwavering support of my mentor, Nathan Goldbaum. I'm deeply grateful to the entire NumPy community for their support and insights, with particular thanks to Sebastian Berg and Nathan for their prior work on NumPy's DType-API, which laid the foundation for this project.

Special appreciation goes to Ralf Gommers, Melissa Weber Mendonça and whole Quansight community for providing this unique opportunity to contribute to NumPy. This experience has been both humbling and inspiring, and I'm excited to see how numpy_quaddtype will evolve and be utilized by the community in the future.

In future, I will be actively involved in this project, so please feel free to ping me with any questions, suggestions, or contributions.

References

More articles from our Blog

Bokeh + Playwright

Testing Bokeh's Accessibility: A Web Developer's Experience with a Python Data Library

By Chiemezuo Akujobi

September 30, 2024

Polar bear with a yellow safety helmet and a red hammer on the ground, representing work-in-progress.

Polars Plugins: let's make them easier to use

By Bruno Kind

September 30, 2024